How to solve y”(x)=f(y(x))

Posted on by Maria

This post is exactly what its title suggests.

It turns out that differential equations of the form y”(x)=f(y(x)), where f is any function of your choice (which depends on the function y (x) that you want to solve for, but not on its derivatives), come up a lot in applied maths. And now it may be totally obvious how to solve them, since they only require a not too clever trick, but it can be hard to spot it in the middle of a large problem. I often get stuck on these by not recognizing their general form, and so do my mathematicians friends.

As I said, all you need is a simple trick: Multiply by y'(x)

y''(x)=f(y(x)) \implies y''(x) y'(x)= y'(x) f(y(x)) \implies \frac{1}{2}(y')^2=\int^y f(u)du

where we need an integration constant (to be determined by initial conditions), that we will absorb below.

Then you integrate again and you’re done.

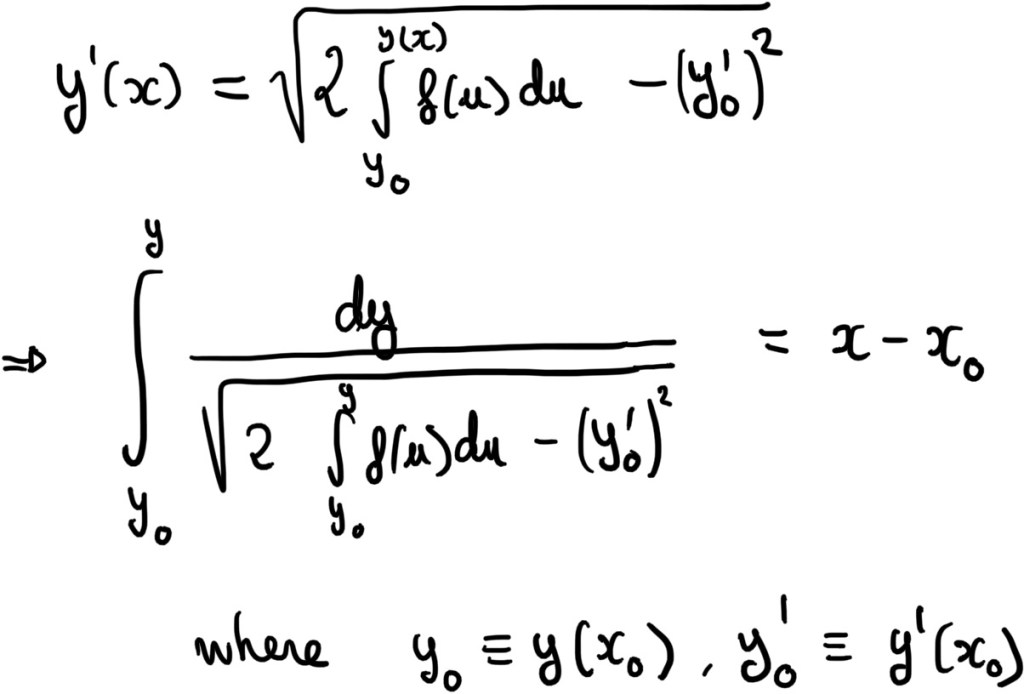
(Writing LaTeX in wordpress is horrible!)

Depending on the example, you may or may not be able to integrate analytically the above, but you can always do it numerically! Actually, you could have used a DE numerical solver from the start, but I think this is neater, and it lets you do other things (eg asymptotics).

Example:

y”=-cos(y)sin(y), y(0)=0, y'(0)=1

\implies y'^2 = \cos^2(y) \implies \int^y_0 dy \sec{y} = \int^x_0 dx

and check that this, with initial conditions, gives

\log{(\tan{y}+\sec{y})} =x

This gives, so far implictitly, y in terms of x.

\exp{x}= \tan{y} + \sec{y} = \tan{y} + \sqrt{1 + \tan^2{y}}

And now I realise I could have chosen an easier example, but at least this could be integrated up. Anyways, it’s now trivial algebra to invert this

e^{2x} -2e^{x}\tan{y} + \tan^2{y}= 1+ \tan^2{y} \implies \tan{y}=\sinh{x}

with solution

y(x) = \arctan{(\sinh{x})}

which should work if plugged into the orginal equation.

Discover more from Maria A. Gutierrez

Subscribe to get the latest posts sent to your email.

Leave a comment